The Circle of Fifths is an extremely useful music theory device which can help you understand pretty much everything about harmony, key signatures, scales and chords. 

It displays the major scales in ascending pitches of perfect fifths (which is where it gets its name from) and then shows how each key is related major to minor, as well as some other juicy music theory tidbits, which we will get into during this guide.

The Circle of Fifths is super useful for creating chord sequences, harmonising melodies and will generally give you a huge boost in know-how when it comes to composing music.

So in this guide we are going to break it down to help you understand exactly what it is, how it works and how you can use it to hack your music making process. 

Let's jump right in!

Understanding Patterns.

Despite what many people say, music theory is interesting. If you consider for a moment whether music was invented or discovered, things start to get really interesting and a little bit weird and existential, so we will stay away from that area.

And just as physicists can use mathematics as a language to explain the solar system, or particles, or the relationships between massive bodies in space, so musicians can use music theory to describe and explain the relationships between sounds.

Music is, after all, just sound. Different notes are just different frequencies in the spectrum, and these notes occur naturally in the world. Everything has a tonality. The human voice, a bird singing, even the noise of wind. 

So again, was music invented or discovered? Weird.

Anyway, you'd be surprised by how much of the music we hear is dictated by a pattern, which is as follows; 

Keys & Tonality

Every single note between C and the C above it has its own major scale, and minor scale. This means that you can pick any note on a keyboard, and starting from that note you can play the major scale pattern we discussed above, and you have a major scale. The same is true for minor scales, and we will discuss the pattern for these a bit later.

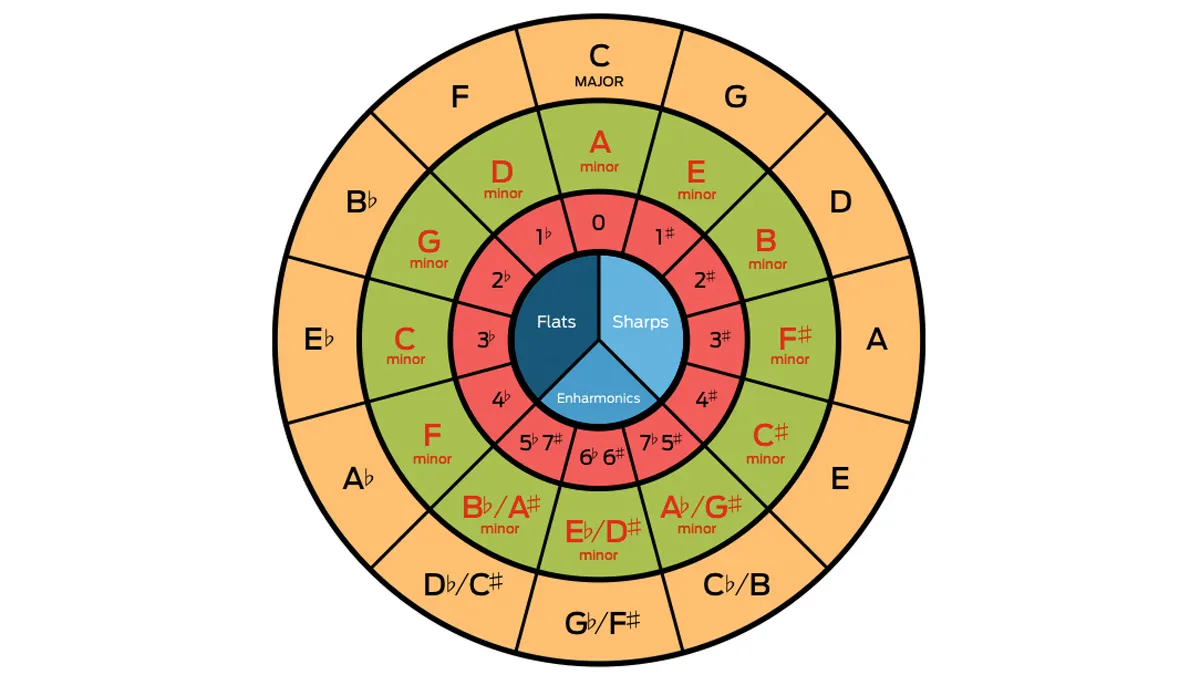
Now, as I'm sure you can imagine, it would be a bit confusing if we just had to instinctively remember what notes are in what key, but luckily, we don't have to. The Circle of Fifths helps us do this, because it describes the relationshis between all of these key signatures and scales. It's a really nice and intuitive way to get everything down in one diagram.

What is really interesting about the circle of fifths is that since there are 12 notes in an octave, it's analagous to a clock. The 12 notes in an octave are each represented by a position we'd recognise corresponding to a time on a 12 hour clock.

I'll be using a lot of 'in the 3 o'clock position' analogies in this guide, so bear that in mind as we move forward!

It was discovered that the fifth note of any given major scale is significant, because all the notes of the fifth note's major scale will line up with those of the first note's major scale, except for one. And this one that doesn't line up is significant.

So, let's start looking at the Circle of Fifths as we go along.

The C Major scale contains no sharp notes or flat notes. (it's all the white notes on a piano keyboard, as we said.)

This is why it's at the top of the circle, and you can see the inner red ring indicating the number of sharps or flats. 

Now, when you take the fifth note of C Major you get G, and the scale of G Major has one sharp note in it; F#. 

If you then take the fifth note of G Major you get D, and the D Major scale contains 2 sharp notes; F# and C#. This continues up the scales. 

There's something interesting about this relationship between scales. Each Major Scale you make from the fifth note of the previous scale, contains one more sharp note in it each time. 

You can see this mapped onto the Circle of Fifths, running clockwise from the 12 o'clock to the 6 o'clock position. 

It's interesting to note that as the sharp notes add up they form a sequence; F C G D A E B, and when reversed, this is the order of flat notes; B E A D G C F. (We will come to flat notes shortly)

The Green ring indicates the relative minor scale of each Major scale, which also contains the same amount of sharp notes. 

So, to quote Pierce Porterfield's wonderful video again;

'As we progress through each fifth note scale, there's a universal order to which notes are sharp and flat. Let's call this The Order of Sharps & Flats'.

 This relationship is interesting, and quite beautiful in my opinion. The way the scales share this relationship is wonderful, and useful because it allows us to plot it for reference.

The Circle of Fifths

This system was plotted onto a circular diagram in the 1600s, the name of which there are no prizes for guessing.

Starting at the top with C Major, we progress around the circle with the next space being taken up by the fifth note major scale, increasing the amount of sharp notes each time. 

So by doing this, you can figure out which notes are sharp in each of the keys, and what's really interesting is the order of sharps we discussed earlier, is present in the outer ring of the circle. Just begin reading it clockwise from the F note at the 11 o'clock position, and you have the order of sharps.

Why do we begin from the F? Because F# is the first sharp note that appears in a scale; G Major, the fifth of C Major.

I realise this is a little complicated, so let me try and explain how it works. 

Each scale (after C Major) has an increasing number of sharp notes. 

If we pick E Major, that sits at the 4 o'clock position on our Circle of Fifths. Now, beginning from F (at the 11 o'clock position), you count 4 places, giving you the following notes;

F, C, G, D.

Now, can you guess what the four sharp notes are in the E Major scale? 

F#, C#, G# & D#.

You can use this logic to figure out not only the amount of sharp notes in any given major scale, but also which notes they are.

Now, we can use this same system to calculate flat notes, but we do need to change how we approach things slightly.

The Order of Flats.

When we reach our 7 o'clock position on the circle of fifths, we reach Db Major. This is where the sharp keys end and the flat keys begin.

We use the same system to figure out the number of flat notes in a scale, but at this 7 position we are starting with 5 flat notes, so it's sort of in reverse.

Let's remind ourself of the order of flats;

B E A D G C F

This is, as we covered earlier, the order of sharps in reverse, and just like the order of sharps, it's present in the circle of fifths diagram for us.

The B which occupies our 5 o'clock position is the first flat note, and if you count back counterclockwise, you have the order of flats! 

So, let's take a scale to figure this out.

Eb Major occupies the 9 o'clock position on our Circle of Fifths. Bearing in mind that we subtract the number of flat notes, because we're working backwards, this means that Eb contains 3 flat notes. 

Now, move over to the B note at our 5 o'clock position, and counting counterclockwise, go back 3 places.

This gives us the notes; B, E, A. 

And the flat notes in Eb Major? Bb, Eb and Ab.

A note on sharps and flats (pun intended).

The whole business with sharps and flats can be confusing, but all it means is to raise or lower a note by half a step.

This means moving a single note on the piano, or in a DAW, one place up or down on the piano roll. 

You'll notice in our circle of fifths that some scales are labelled as both a sharp and a flat. This is because what we call them depends entirely on context. You'll notice in our diagram above, the middle circle contains a bottom section which says 'Enharmonics'. 

The Enharmonic keys are keys with five, six and seven sharps (B, F#, C#), and they overlap with the keys that contains five, six and seven flats (Db, Gb and B). These keys are the same, since F# Major has six sharps, and Gb Major has six flats. These two keys contain the same notes, but have two different names.

The same is true for their relative minors. The Enharmonic Keys have dual identities according to whether you're working with sharps or flats.

The naming convention of the notes in the scale is dependent on that pattern we talked about earlier. 

Each note in a scale is a degree of that scale; the tonic is the first degree, and then we have second through to seventh. 

The circle of fifths is derived from taking a major scale from the fifth degree of a previous scale.

So let's look at the F Major scale, which contains one flat note; Bb.

F G A Bb C D E

This note is also present in other scales as A#, but in this case it is labelled as Bb because in F Major, B is the fourth degree of the scale.

It couldn't be A# because there's already a natural A note in the scale of F Major!

Relative Minors

Hopefully you're still with us at this point. It seems complicated but once you get your head around all the information and see it visualised on the circle of fifths, it's really intuitive and makes a lot sense.

So far we've covered the Major scales and how they progress around the circle using the major scale from the fifth degree of the previous scale. We've also discussed the relationship between the sharps and flats and how they're plotted on the circle of fifths.

Now, let's talk about the the relative minor scales.

We take the fifth degree of a major scale to get the next major scale in the order of sharps. 

Now, if we take the sixth degree of a major scale, and play all the same notes as in the major scale, you get the relative minor. 

A minor scale is dictated by the following pattern; 

Skip, Don't Skip, Skip, Skip, Don't Skip, Skip, Skip

This is the same pattern as the Major scale, just beginning from a different point. This is why if you take a Major scale, play the notes from the major scale but start from the sixth degree instead of the root note, you get that scale's relative minor scale.

This is universal across all scales; the relative minor scale of a major scale is found by playing the above pattern, starting from the sixth degree of the major scale.

These realationships are complex and elegant; the fifth degree of a scale gives the next major scale, and the sixth degree gives the correpsonding minor scale.

Moving on from the basics.

So all of the above is the theory behind how the Circle of Fifths works, what it's describing and how it can help you understand key signatures and scales, and more importantly the relationships between them.

But, believe it or not, the Circle of Fifths can do more.

You can extract the diatonic chords of each key from the Circle of Fifths.

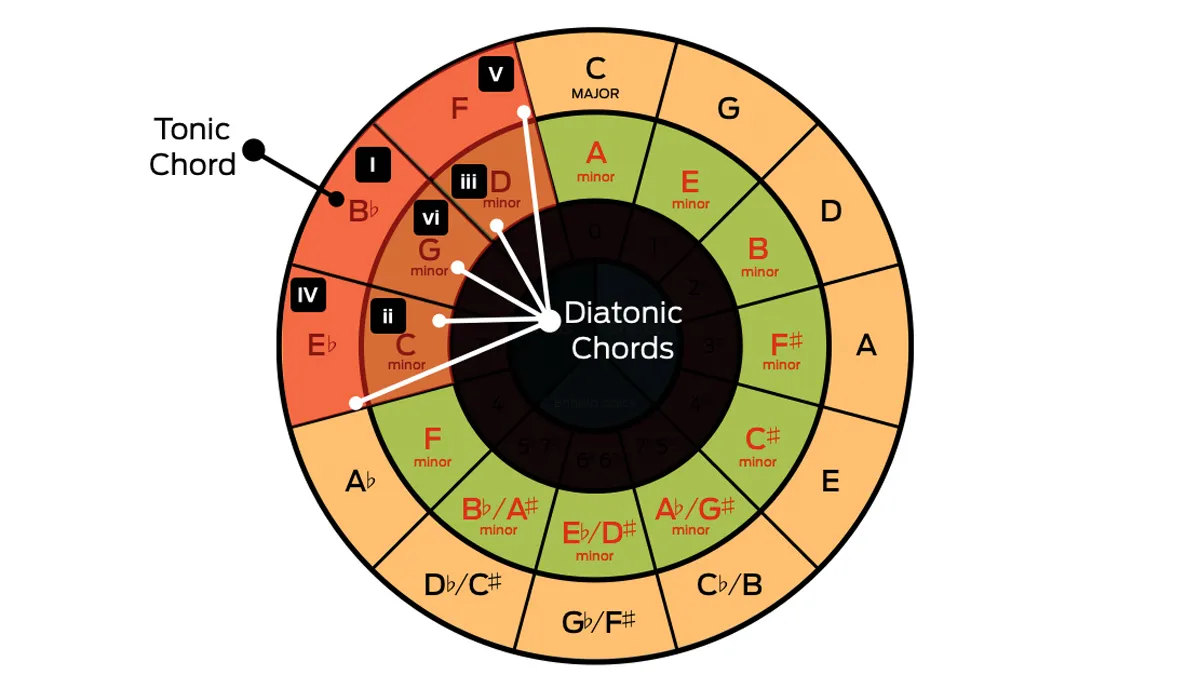
 Each scale contains seven notes, and from each note in a scale, you can then construct chords using notes from the scale. This gives each note in the scale its own chord, and these are numbered.

If you take a particular note for your major scale, that note will also be the tonic chord. So in the example above, the Bb note is your chord of Bb Major.

The two blocks either side of the tonic will always be your fourth on the left and fifth on the right. 

These are known as the primary chords, and the I - IV - V chord progression is ubiquitously popular in pop music. There are literally thousands of songs which use this chord sequence. 

You can then add in the relative minor chords, which are the ii - vi & iii chords. You can see these on the diagram above too. These are always in the same position relative to the blocks you've chosen for your tonic scale. 

So directly under the tonic is the vi chord, and to the left is the ii and to the right is the iii.

So this is a great way to instantly figure out a key signature, what its relative minor is, and also what chords are present in that key.

Do you see how the Circle of Fifths is becoming more and more useful in its application to your music writing the more you learn about it?

An Overview

So, as we've seen, the Circle of Fifths is a really useful tool which can help you figuring out a lot when it comes to the harmonic and theory side of music. 

This is a really good first port of call for learning music theory; it gives you an overview of all of the different keys you could be working in, and understanding the relationships between them is the first step on the road to gaining a more fundamental grasp of how music works and fits together. 

It's a good thing to have printed out and on the wall near where you make your music, because it's a good visual reference. In this guide we've covered how you can use it to figure out the chords in keys, their relative minors, and the amount of sharp or flat notes they each contain.

So, hopefully you got something useful out of this guide, and now you should be able to apply this to your own music making and ensure you're making more key-conscious decisions when writing music.

Thanks for checking in with us here at Top Music Arts. While you're here, be sure to check out our collection of Ableton Live Project Templates, where you're bound to find a good deal on a track you know really well. We have an international team of producers working to re-create chart topping EDM tracks in studio quality detail, meaning you get to have a hands on dive through all of the tricks that make a professional track stand out.